Visualizing Quantum Gates- Bloch Sphere

Introduction

Quantum gates are the building blocks of quantum circuits, analogous to classical logic gates in conventional digital circuits. They operate on a small number of qubits and are reversible, preserving the quantum state information. In this article, we will explore the key differences between quantum gates and classical gates, the different types of quantum gates, their Bloch representation, and a comparison with classical gates.

Differences between Quantum Gates and Classical Gates

Quantum gates differ significantly from their classical counterparts in the following ways:

• Superposition: Quantum gates can manipulate qubits in superposition, allowing for simultaneous exploration of multiple states.
• Entanglement: Quantum gates exploit entanglement, where the state of one qubit is intrinsically linked to another, even when separated by large distances.
• Unitarity: Quantum gates are unitary transformations, meaning they preserve the norm of the quantum state vector.
• Interference: Quantum gates exploit quantum interference to enhance or reduce the probability of certain outcomes, while classical gates do not have this feature.

Quantum Gates

Quantum gates are reversible operations applied to one or more qubits. They change the state of the quantum qubit and are represented by unitary matrices. The most common quantum gates operate on vector spaces of one or two qubits, just like the common classical logic gates operate on one or two bits.

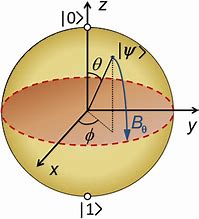
Bloch Sphere Representation

The Bloch sphere provides an intuitive visualization of quantum states. It’s a 3D representation where:

• The x, y, and z axes correspond to the real and imaginary parts of the quantum state.
• Each point on the sphere represents a quantum state.
• Quantum gates act as rotations on this sphere, transforming the state vector.
  

  

Different Types of Quantum Gates

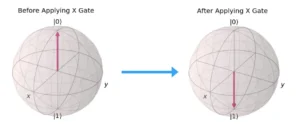
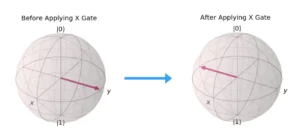
1. Pauli-X Gate
   • Symbol: σₓ
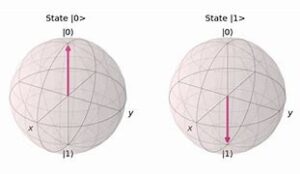
   • Effect: Flips the state of a qubit (|0⟩ becomes |1⟩ and vice versa).
   • Matrix Representation: A 180º rotation about the x-axis on the Bloch sphere.
   • Mathematical Representation: Flip of |0> using Pauli X Gate:

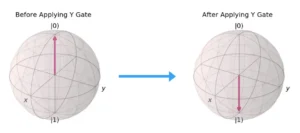
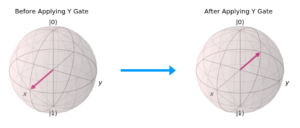
2. Pauli-Y Gate
   • Symbol: σᵧ
   • Effect: Rotates the state vector around the y-axis.
   • Matrix Representation: A combination of phase shift and flip.
   • Example: The quantum state must flip over the X-Y plane, or in other words, θ’=π-θ. The quantum state must flip over the Y-Z plane, or in other words, φ’=π-φ.
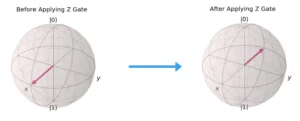
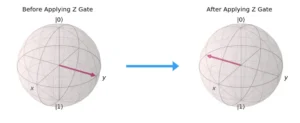
3. Pauli-Z Gate
   • Symbol:σ_z
   • Effect: Flips the sign of the state of a qubit.
   • Matrix Representation: A 180º rotation about the z-axis on the Bloch sphere.
   • Mathematical Representation: Flip of |0> using Pauli Z Gate:
     

     

     

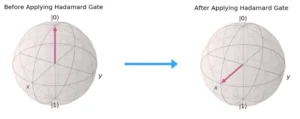
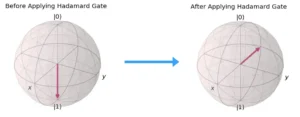
4. Hadamard Gate
   • Symbol: H
   • Effect: Creates a superposition of states.
   • Matrix Representation: A rotation of 90º about the axis between the X and Z axes on the Bloch sphere.
   • Mathematical Representation:

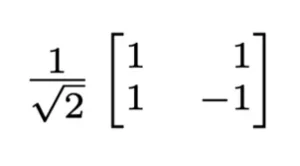
Comparison with Classical Gates

Quantum gates offer several advantages over classical gates, including:

• Utilizes qubits to represent and process information.
• Leverages quantum superposition and entanglement.
• Offers the potential for exponential computational speedup.
• Can solve complex problems such as factorization and optimization.

However, quantum gates are limited by the constraints of classical physics and require specialized hardware and algorithms. They are well-suited for traditional computing tasks and can be used to enhance the performance of classical computers. We hope that technological advancement in cryogenics and superconductor technology will push forward Quantum advantage.

Click here for latest Quantum Computing Developments.

Click here to learn Mathematics on Quantum Gates.