Introduction
Achieving optimal performance in the field of control systems requires a deep understanding of the dynamics of various damping scenarios. Damping refers to a system’s ability to dissipate energy and regulate its response to external influences. By comprehending the characteristics of underdamped, overdamped, and critically damped systems, engineers can design control strategies that ensure stability and efficiency.
Basics of Control Systems
Before exploring damping dynamics, it is essential to grasp the fundamentals of control systems. A control system consists of interconnected elements that work together to regulate the behavior of a physical process or system. These elements include sensors, actuators, controllers, and feedback loops. Damping plays a significant role in controlling the system’s response, determining the rate at which oscillations decay over time. Understanding damping is vital for achieving stability and avoiding undesirable behaviors, such as excessive oscillations or sluggish responses.
Underdamped Systems
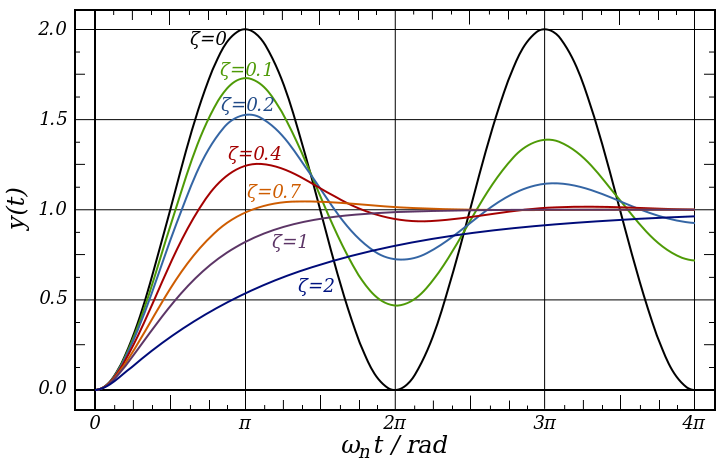
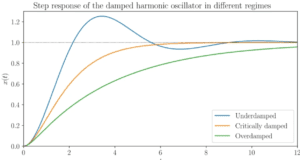
Underdamped systems display oscillatory responses when subjected to external forces or disturbances. These systems possess a damped natural frequency, which refers to the rate at which oscillations decay. The damped natural frequency is lower than the undamped natural frequency, indicating a gradual damping of the system’s oscillations. The transfer function representation of an underdamped system includes complex poles, indicating the presence of oscillatory behavior. Underdamped systems find applications in various fields, including mechanical vibrations, electrical circuits, and control of robotic manipulators.
The transfer function representation of an underdamped system can be expressed in terms of a second-order linear differential equation. For an underdamped system, the transfer function has two complex conjugate poles. The general form of the transfer function for an underdamped second-order system is given as:
T(s)=K/[(s−α)2+ωd2]
where:
- T(s) is the transfer function,
- K is the system gain,
- α is the real part of the complex poles,
- ωd is the damping frequency.
The poles of the transfer function (α±jωd) are determined by the damping ratio (ζ) and natural frequency (ωn) of the system. The relationship between ζ, ωn, and ωd is given by:
ωd=ωn[1−ζ2]1/2
α=−ζωn
Here, ωn is the natural frequency of the system.
In an underdamped system, the damping ratio ( ζ) is less than 1, and the system exhibits oscillatory behavior. The parameter determines the level of damping in the system, with lower values of resulting in more pronounced oscillations.
Overdamped Systems
In contrast to underdamped systems, overdamped systems have slow responses without oscillations. Strong damping characterizes overdamped systems, causing them to take a significant amount of time to reach their steady-state condition. This intentional introduction of excessive damping ensures a slow response while preventing oscillations. The transfer function representation of an overdamped system consists of real poles without any complex components. Overdamped behavior is observed in applications such as shock absorbers, fluid dynamics, and thermal management systems.
The transfer function representation of an overdamped system can be expressed in terms of a second-order linear differential equation. For an overdamped system, the transfer function has two real distinct poles. The general form of the transfer function for an overdamped second-order system is given as:
T(s) = K/[(s−α)(s−β)]
where:
- T(s) is the transfer function,
- K is the system gain,
- α and β are the real distinct poles.
The poles α and β are determined by the characteristics of the system, such as the damping ratio (ζ) and natural frequency (ωn). The damping ratio for an overdamped system is greater than 1 (ζ>1), and the poles are given by:
α=−ζωn+[ζ2−1]1/2ωn
β=−ζωn–[ζ2−1]1/2ωn
Here, ωn is the natural frequency of the system.
Critically Damped Systems
Critically damped systems provide the fastest response without any oscillations. They strike a balance between underdamped and overdamped systems, ensuring quick settling time without overshooting the setpoint. Critically damped systems offer optimal performance when stringent control requirements, such as precise positioning or stability, are necessary. The transfer function representation of a critically damped system includes real but repeated poles. Critically damped systems find applications in industries such as aerospace, robotics, and industrial automation.
For a critically damped system, the transfer function has two real and identical poles. The general form of the transfer function for a critically damped second-order system is given as:
T(s)=K/(s+α)2</sup
where:
- T(s) is the transfer function,
- K is the system gain,
- α is the real part of the double pole.
The double pole α is determined by the damping ratio (ζ) and natural frequency (ωn) of the system. The relationship between ζ and ωn for a critically damped system is:
α=−ζωn
Here, ωn is the natural frequency of the system.
In a critically damped system, the damping ratio (ζ) is equal to 1, and the system response does not exhibit oscillatory behavior. The response is the fastest among the three damping scenarios, settling to the desired state with minimal overshooting.
DoFollow for some other information regarding damping. Click Here
Control Strategies for Different Damping Scenarios
Engineers employ various strategies and techniques to achieve effective control in different damping scenarios. One commonly used control strategy is the Proportional-Integral-Derivative (PID) controller. This controller adjusts the system’s output based on the proportional, integral, and derivative terms, allowing for precise control and stability.
When dealing with underdamped systems, tuning parameters are crucial for maintaining stability and desired performance. Engineers must carefully adjust the gain and time constants to prevent overshooting and excessive oscillations.
In overdamped systems, selecting the appropriate damping constants is essential to avoid unnecessarily slow responses. Adjusting the damping parameters allows engineers to optimize the system’s behavior for the desired application.
For critically damped systems, achieving optimal performance involves fine-tuning the damping constants to strike a balance between response time and settling time. Careful consideration of the damping characteristics is necessary to maintain stability while quickly reaching the desired state.
Practical Implementations
Real-world control system applications often present unique challenges. Understanding the characteristics of different damping scenarios enables engineers to tailor control strategies to specific applications. Case studies in areas such as power plants, autonomous vehicles, and manufacturing processes demonstrate the importance of selecting the right damping characteristics.
Addressing challenges and finding solutions in real-world scenarios requires a deep understanding of control system dynamics. By mastering the intricacies of different damping scenarios, engineers can design systems that meet performance goals while ensuring stability and reliability.
Future Trends and Advancements
Advancements in technology present new opportunities for control systems. The integration of artificial intelligence and machine learning algorithms within control systems opens up possibilities for efficient and adaptive control. These advancements enable control systems to learn from data, adapt to changing conditions, and continuously optimize their response. The potential improvements in system response and efficiency have the ability to revolutionize industries such as robotics, autonomous systems, and advanced manufacturing.
Conclusion
Understanding the dynamics of underdamped, overdamped, and critically damped systems is crucial for achieving optimal control performance. By comprehending the characteristics and behaviors of different damping scenarios, engineers can design control strategies that ensure stability, efficiency, and precision.
Mastering the principles of control dynamics is essential for successful applications in industries ranging from aerospace to robotics. As technology evolves and new challenges arise, continued research and exploration in control systems will pave the way for innovative solutions and further advancements in the field.